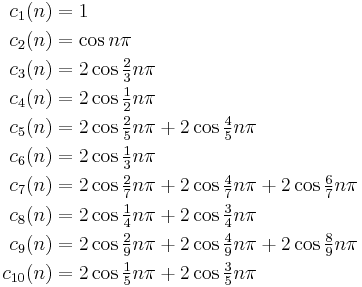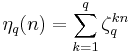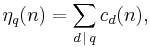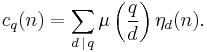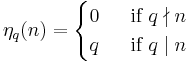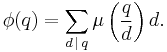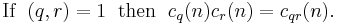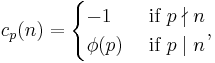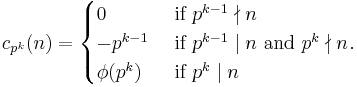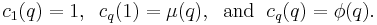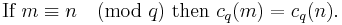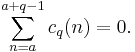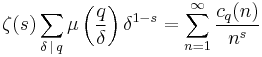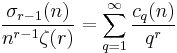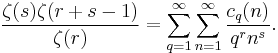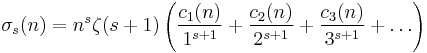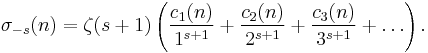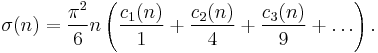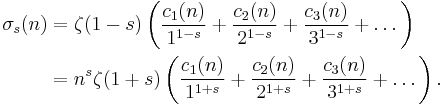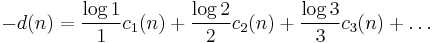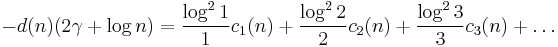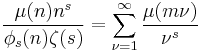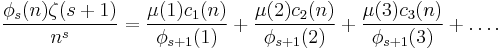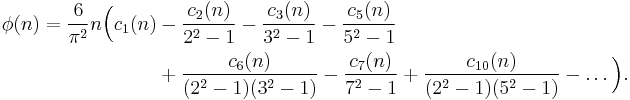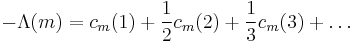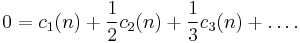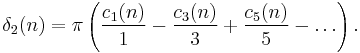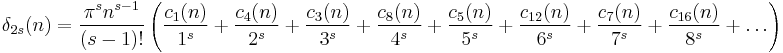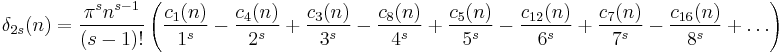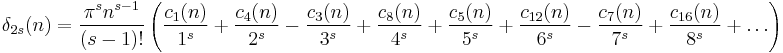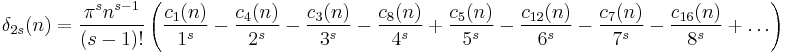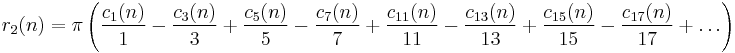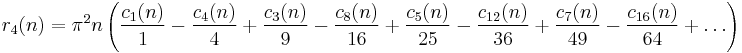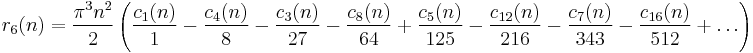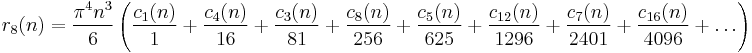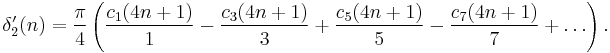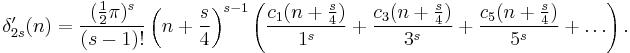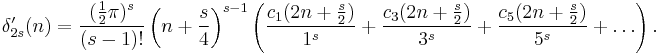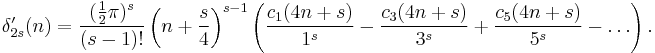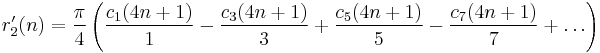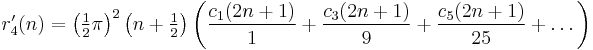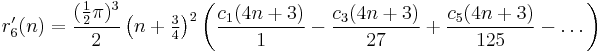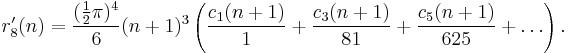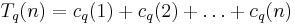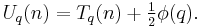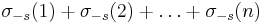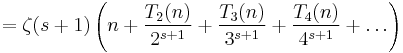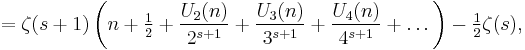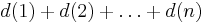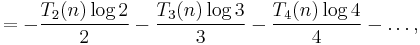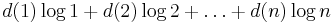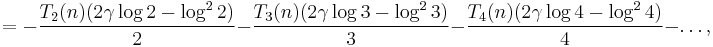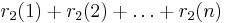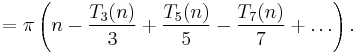Ramanujan's sum
- This article is not about Ramanujan summation.
In number theory, a branch of mathematics, Ramanujan's sum, usually denoted cq(n), is a function of two positive integer variables q and n defined by the formula
where (a, q) = 1 means that a only takes on values coprime to q.
Srinivasa Ramanujan introduced the sums in a 1918 paper.[1] In addition to the expansions discussed in this article, Ramanujan's sums are used in the proof of Vinogradov's theorem that every sufficiently-large odd number is the sum of three primes.[2]
Contents |
Notation
For integers a and b, 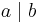 is read "a divides b" and means that there is an integer c such that b = ac. Similarly,
is read "a divides b" and means that there is an integer c such that b = ac. Similarly, 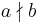 is read "a does not divide b". The summation symbol
is read "a does not divide b". The summation symbol 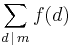 means that d goes through all the positive divisors of m, e.g.
means that d goes through all the positive divisors of m, e.g.
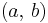 is the greatest common divisor,
is the greatest common divisor,
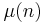 is the Möbius function, and
is the Möbius function, and
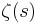 is the Riemann zeta function.
is the Riemann zeta function.
Formulas for cq(n)
Trigonometric
These formulas come from the definition, Euler's formula 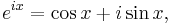 and elementary trigonometric identities.
and elementary trigonometric identities.
and so on ( A000012, A033999, A099837, A176742,.., A100051,...) They show that cq(n) is always real.
Kluyver
Let 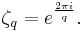
Then ζq is a root of the equation xq – 1 = 0. Each of its powers ζq, ζq2, ... ζqq = ζq0 = 1 is also a root. Therefore, since there are q of them, they are all of the roots. The numbers ζqn where 1 ≤ n ≤ q are called the qth roots of unity. ζq is called a primitive q th root of unity because the smallest value of n that makes ζqn = 1 is q. The other primitive qth roots of are the numbers ζqa where (a, q) = 1. Therefore, there are φ(q) primitive q th roots of unity.
Thus, the Ramanujan sum cq(n) is the sum of the n th powers of the primitive q th roots of unity.
It is a fact[3] that the powers of ζq are precisely the primitive roots for all the divisors of q.
For example, let q = 12. Then
- ζ12, ζ125, ζ127, and ζ1211 are the primitive twelfth roots of unity,
- ζ122 and ζ1210 are the primitive sixth roots of unity,
- ζ123 = i and ζ129 = −i are the primitive fourth roots of unity,
- ζ124 and ζ128 are the primitive third roots of unity,
- ζ126 = −1 is the primitive second root of unity, and
- ζ1212 = 1 is the primitive first root of unity.
Therefore, if
is the sum of the n th powers of all the roots, primitive and imprimitive,
and by Möbius inversion,
It follows from the identity xq – 1 = (x – 1)(xq–1 + xq–2 + ... + x + 1) that
and this leads to the formula
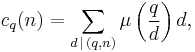 published by Kluyver in 1906.[4]
published by Kluyver in 1906.[4]
This shows that cq(n) is always an integer. Compare it with the formula
von Sterneck
It is easily shown from the definition that cq(n) is multiplicative when considered as a function of q for a fixed value of n: i.e.
From the definition (or Kluyver's formula) it is straightforward to prove that, if p is a prime number,
and if pk is a prime power where k > 1,
This result and the multiplicative property can be used to prove
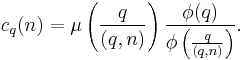 This is called von Sterneck's arithmetic function.[5]
This is called von Sterneck's arithmetic function.[5]
The equivalence of it and Ramanujan's sum is due to Hölder.[6][7]
Other properties of cq(n)
For all positive integers q,
For a fixed value of q the absolute value of the sequence
- cq(1), cq(2), ... is bounded by φ(q), and
for a fixed value of n the absolute value of the sequence
- c1(n), c2(n), ... is bounded by σ(n), the sum of the divisors of n.
If q > 1
Table
| n | |||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | ||
| s | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 2 | −1 | 1 | −1 | 1 | −1 | 1 | −1 | 1 | −1 | 1 | −1 | 1 | −1 | 1 | −1 | 1 | −1 | 1 | −1 | 1 | −1 | 1 | −1 | 1 | −1 | 1 | −1 | 1 | −1 | 1 | |
| 3 | −1 | −1 | 2 | −1 | −1 | 2 | −1 | −1 | 2 | −1 | −1 | 2 | −1 | −1 | 2 | −1 | −1 | 2 | −1 | −1 | 2 | −1 | −1 | 2 | −1 | −1 | 2 | −1 | −1 | 2 | |
| 4 | 0 | −2 | 0 | 2 | 0 | −2 | 0 | 2 | 0 | −2 | 0 | −2 | 0 | 2 | 0 | −2 | 0 | 2 | 0 | −2 | 0 | −2 | 0 | 2 | 0 | −2 | 0 | 2 | 0 | −2 | |
| 5 | −1 | −1 | −1 | −1 | 4 | −1 | −1 | −1 | −1 | 4 | −1 | −1 | −1 | −1 | 4 | −1 | −1 | −1 | −1 | 4 | −1 | −1 | −1 | −1 | 4 | −1 | −1 | −1 | −1 | 4 | |
| 6 | 1 | −1 | −2 | −1 | 1 | 2 | 1 | −1 | −2 | −1 | 1 | 2 | 1 | −1 | −2 | −1 | 1 | 2 | 1 | −1 | −2 | −1 | 1 | 2 | 1 | −1 | −2 | −1 | 1 | 2 | |
| 7 | −1 | −1 | −1 | −1 | −1 | −1 | 6 | −1 | −1 | −1 | −1 | −1 | −1 | 6 | −1 | −1 | −1 | −1 | −1 | −1 | 6 | −1 | −1 | −1 | −1 | −1 | −1 | 6 | −1 | −1 | |
| 8 | 0 | 0 | 0 | −4 | 0 | 0 | 0 | 4 | 0 | 0 | 0 | −4 | 0 | 0 | 0 | 4 | 0 | 0 | 0 | −4 | 0 | 0 | 0 | 4 | 0 | 0 | 0 | −4 | 0 | 0 | |
| 9 | 0 | 0 | −3 | 0 | 0 | −3 | 0 | 0 | 6 | 0 | 0 | −3 | 0 | 0 | −3 | 0 | 0 | 6 | 0 | 0 | −3 | 0 | 0 | −3 | 0 | 0 | 6 | 0 | 0 | −3 | |
| 10 | 1 | −1 | 1 | −1 | −4 | −1 | 1 | −1 | 1 | 4 | 1 | −1 | 1 | −1 | −4 | −1 | 1 | −1 | 1 | 4 | 1 | −1 | 1 | −1 | −4 | −1 | 1 | −1 | 1 | 4 | |
| 11 | −1 | −1 | −1 | −1 | −1 | −1 | −1 | −1 | −1 | −1 | 10 | −1 | −1 | −1 | −1 | −1 | −1 | −1 | −1 | −1 | −1 | 10 | −1 | −1 | −1 | −1 | −1 | −1 | −1 | −1 | |
| 12 | 0 | 2 | 0 | −2 | 0 | −4 | 0 | −2 | 0 | 2 | 0 | 4 | 0 | 2 | 0 | −2 | 0 | −4 | 0 | −2 | 0 | 2 | 0 | 4 | 0 | 2 | 0 | −2 | 0 | −4 | |
| 13 | −1 | −1 | −1 | −1 | −1 | −1 | −1 | −1 | −1 | −1 | −1 | −1 | 12 | −1 | −1 | −1 | −1 | −1 | −1 | −1 | −1 | −1 | −1 | −1 | −1 | 12 | −1 | −1 | −1 | −1 | |
| 14 | 1 | −1 | 1 | −1 | 1 | −1 | −6 | −1 | 1 | −1 | 1 | −1 | 1 | 6 | 1 | −1 | 1 | −1 | 1 | −1 | −6 | −1 | 1 | −1 | 1 | −1 | 1 | 6 | 1 | −1 | |
| 15 | 1 | 1 | −2 | 1 | −4 | −2 | 1 | 1 | −2 | −4 | 1 | −2 | 1 | 1 | 8 | 1 | 1 | −2 | 1 | −4 | −2 | 1 | 1 | −2 | −4 | 1 | −2 | 1 | 1 | 8 | |
| 16 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | −8 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 8 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | −8 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 17 | −1 | −1 | −1 | −1 | −1 | −1 | −1 | −1 | −1 | −1 | −1 | −1 | −1 | −1 | −1 | −1 | 16 | −1 | −1 | −1 | −1 | −1 | −1 | −1 | −1 | −1 | −1 | −1 | −1 | −1 | |
| 18 | 0 | 0 | 3 | 0 | 0 | −3 | 0 | 0 | −6 | 0 | 0 | −3 | 0 | 0 | 3 | 0 | 0 | 6 | 0 | 0 | 3 | 0 | 0 | −3 | 0 | 0 | −6 | 0 | 0 | −3 | |
| 19 | −1 | −1 | −1 | −1 | −1 | −1 | −1 | −1 | −1 | −1 | −1 | −1 | −1 | −1 | −1 | −1 | −1 | −1 | 18 | −1 | −1 | −1 | −1 | −1 | −1 | −1 | −1 | −1 | −1 | −1 | |
| 20 | 0 | 2 | 0 | −2 | 0 | 2 | 0 | −2 | 0 | −8 | 0 | −2 | 0 | 2 | 0 | −2 | 0 | 2 | 0 | 8 | 0 | 2 | 0 | −2 | 0 | 2 | 0 | −2 | 0 | −8 | |
| 21 | 1 | 1 | −2 | 1 | 1 | −2 | −6 | 1 | −2 | 1 | 1 | −2 | 1 | −6 | −2 | 1 | 1 | −2 | 1 | 1 | 12 | 1 | 1 | −2 | 1 | 1 | −2 | −6 | 1 | −2 | |
| 22 | 1 | −1 | 1 | −1 | 1 | −1 | 1 | −1 | 1 | −1 | −10 | −1 | 1 | −1 | 1 | −1 | 1 | −1 | 1 | −1 | 1 | 10 | 1 | −1 | 1 | −1 | 1 | −1 | 1 | −1 | |
| 23 | −1 | −1 | −1 | −1 | −1 | −1 | −1 | −1 | −1 | −1 | −1 | −1 | −1 | −1 | −1 | −1 | −1 | −1 | −1 | −1 | −1 | −1 | 22 | −1 | −1 | −1 | −1 | −1 | −1 | −1 | |
| 24 | 0 | 0 | 0 | 4 | 0 | 0 | 0 | −4 | 0 | 0 | 0 | −8 | 0 | 0 | 0 | −4 | 0 | 0 | 0 | 4 | 0 | 0 | 0 | 8 | 0 | 0 | 0 | 4 | 0 | 0 | |
| 25 | 0 | 0 | 0 | 0 | −5 | 0 | 0 | 0 | 0 | −5 | 0 | 0 | 0 | 0 | −5 | 0 | 0 | 0 | 0 | −5 | 0 | 0 | 0 | 0 | 20 | 0 | 0 | 0 | 0 | −5 | |
| 26 | 1 | −1 | 1 | −1 | 1 | −1 | 1 | −1 | 1 | −1 | 1 | −1 | −12 | −1 | 1 | −1 | 1 | −1 | 1 | −1 | 1 | −1 | 1 | −1 | −1 | 12 | 1 | −1 | 1 | −1 | |
| 27 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | −9 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | −9 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 18 | 0 | 0 | 0 | |
| 28 | 0 | 2 | 0 | −2 | 0 | 2 | 0 | −2 | 0 | 2 | 0 | −2 | 0 | −12 | 0 | −2 | 0 | 2 | 0 | −2 | 0 | 2 | 0 | −2 | 0 | 2 | 0 | 12 | 0 | 2 | |
| 29 | −1 | −1 | −1 | −1 | −1 | −1 | −1 | −1 | −1 | −1 | −1 | −1 | −1 | −1 | −1 | −1 | −1 | −1 | −1 | −1 | −1 | −1 | −1 | −1 | −1 | −1 | −1 | −1 | 28 | −1 | |
| 30 | −1 | 1 | 2 | 1 | 4 | −2 | −1 | 1 | 2 | −4 | −1 | −2 | −1 | 1 | −8 | 1 | −1 | −2 | −1 | −4 | 2 | 1 | −1 | −2 | 4 | 1 | 2 | 1 | −1 | 8 | |
Ramanujan expansions
If f(n) is an arithmetic function (i.e. a complex-valued function of the integers or natural numbers), then a convergent infinite series of the form
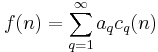 or of the form
or of the form
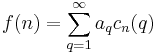 (where the aq are complex numbers),
(where the aq are complex numbers),
is called a Ramanujan expansion[8] of f(n). .
Ramanujan found expansions of some of the well-known functions of number theory. All of these results are proved in an "elementary" manner (i.e. only using formal manipulations of series and the simplest results about convergence).[9][10][11]
The expansion of the zero function depends on a result from the analytic theory of prime numbers, namely that the series 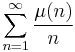 converges to 0, and the results for r(n) and r′(n) depend on theorems in an earlier paper.[12]
converges to 0, and the results for r(n) and r′(n) depend on theorems in an earlier paper.[12]
All the formulas in this section are from Ramanujan's 1918 paper.
Generating functions
The generating functions of the Ramanujan sums are Dirichlet series:
is a generating function for the sequence cq(1), cq(2), ... where q is kept constant, and
is a generating function for the sequence c1(n), c2(n), ... where n is kept constant.
There is also the double Dirichlet series
σk(n)
σk(n) is the divisor function (i.e. the sum of the kth powers of the divisors of n, including 1 and n). σ0(n), the number of divisors of n, is usually written d(n) and σ1(n), the sum of the divisors of n, is usually written σ(n).
If s > 0,
and
Setting s = 1 gives
If the Riemann hypothesis is true, and 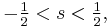
d(n)
d(n) = σ0(n) is the number of divisors of n, including 1 and n itself.
and
where γ = 0.5772... is the Euler–Mascheroni constant.
φ(n)
Euler's totient function φ(n) is the number of positive integers less than n and coprime to n.
Ramanujan defines a generalization of it: if 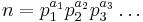 is the prime factorization of n, and s is a complex number, let
is the prime factorization of n, and s is a complex number, let
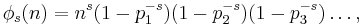 so that φ1(n) = φ(n) is Euler's function.[13]
so that φ1(n) = φ(n) is Euler's function.[13]
He proves that
and uses this to show that
Letting s = 1,
Note that the constant is the inverse[14] of the one in the formula for σ(n).
Λ(n)
Von Mangoldt's function Λ(n) is zero unless n = pk is a power of a prime number, in which case it is the natural logarithm log p.
Zero
For all n > 0,
This is equivalent to the prime number theorem.[15][16]
r2s(n) (sums of squares)
r2s(n) is the number of way of representing n as the sum of 2s squares, counting different orders and signs as different (e.g., r2(13) = 8, as 13 = (±2)2 + (±3)2 = (±3)2 + (±2)2.)
Ramanujan defines a function δ2s(n) and references a paper[17] in which he proved that r2s(n) = δ2s(n) for s = 1, 2, 3, and 4. For s > 4 he shows that δ2s(n) is a good approximation to r2s(n).
s = 1 has a special formula:
In the following formulas the signs repeat with a period of 4.
If s ≡ 0 (mod 4),
If s ≡ 2 (mod 4),
If s ≡ 1 (mod 4) and s > 1,
If s ≡ 3 (mod 4),
and therefore,
r′2s(n) (sums of triangles)
r′2s(n) is the number of ways n can be represented as the sum of 2s triangular numbers (i.e. the numbers 1, 3 = 1 + 2, 6 = 1 + 2 + 3, 10 = 1 + 2 + 3 + 4, 15, ...; the nth triangular number is given by the formula n(n + 1)/2.)
The analysis here is similar to that for squares. Ramanujan refers to the same paper as he did for the squares, where he showed that there is a function δ′2s(n) such that r′2s(n) = δ′2s(n) for s = 1, 2, 3, and 4, and that for s > 4, δ′2s(n) is a good approximation to r′2s(n).
Again, s = 1 requires a special formula:
If s is a multiple of 4,
If s is twice an odd number,
If s is an odd number and s > 1,
Therefore,
Sums
Let
and
Then if s > 1,
See also
Notes
- ^ Ramanujan, On Certain Trigonometric Sums ...
(Papers, p. 179). In a footnote cites pp. 360–370 of the Dirichlet-Dedekind Vorlesungen über Zahlentheorie, 4th ed.These sums are obviously of great interest, and a few of their properties have been discussed already. But, so far as I know, they have never been considered from the point of view which I adopt in this paper; and I believe that all the results which it contains are new.
- ^ Nathanson, ch. 8
- ^ Hardy & Wright, Thms 65, 66
- ^ G. H. Hardy, P. V. Seshu Aiyar, & B. M. Wilson, notes to On certain trigonometrical sums ..., Ramanujan, Papers, p. 343
- ^ B. Berndt, commentary to On certain trigonometrical sums..., Ramanujan, Papers, p. 371
- ^ Knopfmacher, p. 196
- ^ Hardy & Wright, p. 243
- ^ B. Berndt, commentary to On certain trigonometrical sums..., Ramanujan, Papers, pp. 369–371
- ^ Ramanujan, On certain trigonometrical sums...
(Papers, p. 179)The majority of my formulae are "elementary" in the technical sense of the word — they can (that is to say) be proved by a combination of processes involving only finite algebra and simple general theorems concerning infinite series
- ^ The theory of formal Dirichlet series is discussed in Hardy & Wright, § 17.6 and in Knopfmacher.
- ^ Knopfmacher, ch. 7, discusses Ramanujan expansions as a type of Fourier expansion in an inner product space which has the cq as an orthogonal basis.
- ^ Ramanujan, On Certain Arithmetical Functions
- ^ This is Jordan's totient function, Js(n).
- ^ Cf. Hardy & Wright, Thm. 329, which states that
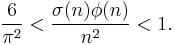
- ^ Hardy, Ramanujan, p. 141
- ^ B. Berndt, commentary to On certain trigonometrical sums..., Ramanujan, Papers, p. 371
- ^ Ramanujan, On Certain Arithmetical Functions
References
- Hardy, G. H. (1999), Ramanujan: Twelve Lectures on Subjects Suggested by his Life and Work, Providence RI: AMS / Chelsea, ISBN 978-0821820230
- Hardy, G. H.; Wright, E. M. (1980), An Introduction to the Theory of Numbers (Fifth edition), Oxford: Oxford University Press, ISBN 978-0198531715
- Knopfmacher, John (1990), Abstract Analytic Number Theory, New York: Dover, ISBN 0-486-66344-2
- Nathanson, Melvyn B. (1996), Additive Number Theory: the Classical Bases, Graduate Texts in Mathematics, 164, Springer-Verlag, ISBN 0-387-94656-X Section A.7.
- Ramanujan, Srinivasa (1918), "On Certain Trigonometric Sums and their Applications in the Theory of Numbers", Transactions of the Cambridge Philosophical Society 22 (15): 259–276 (pp. 179–199 of his Collected Papers)
- Ramanujan, Srinivasa (1916), "On Certain Arithmetical Functions", Transactions of the Cambridge Philosophical Society 22 (9): 159–184 (pp. 136–163 of his Collected Papers)
- Ramanujan, Srinivasa (2000), Collected Papers, Providence RI: AMS / Chelsea, ISBN 978-0821820766
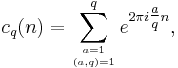
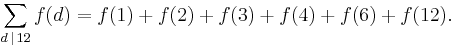
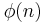 is
is